Practical PowerShell: Where do I start?
This post is the first in a series on PowerShell scripting for the SysAdmin who doesn’t know where to begin. This series is designed to move quickly from PowerShell basics to advanced scripting techniques. It is meant as a guide, not a standalone resource.
“So, where do I begin?”
You really thought I was going to start this post by shattering the third wall and asking a self-referential question? I wasn’t.
I was reading your mind.
There are two common refrains I have heard from people about PowerShell. The first is simple, “I want to learn PowerShell.” Support team members and young systems administrators know that the best way to learn a new role and grow their career is by learning a new skillset. PowerShell is becoming one of the most important and empowering skills that an aspiring administrator or engineer can learn.
The other statement is always tinged with a bit of regret, “I really wish I would have learned PowerShell sooner.” For any number of reasons many seasoned IT Pros have waited to learn PowerShell. It may not have been relevant to the systems they worked on, perhaps they had a preferred scripting language, or could complete most tasks through a GUI. In a cloud first world development cycles have been shortened and not every function finds its way into a GUI. Most systems administrators eventually find a need for PowerShell, and in the end, regret not using it sooner.
There’s one underlying principle in both cases – people don’t know where to begin with PowerShell. It’s a massive topic. There are countless resources available – from user groups, to video series, tutorials, and books. I will include a few links to some of those tools at the bottom, and if anyone has other links they would like to share I would be happy to add them. If you have the time to sit down and digest in-depth content on PowerShell I would highly recommend diving into some of the more advanced content written by experts in our field.
I wouldn’t consider myself an expert in PowerShell. I’m an IT Pro who had a need, and like many other IT Pros I didn’t know where to begin. I began my systems administration journey in a role that required me to learn WiseScript and AutoIT. I had a basic understanding of VBScript and .Net. PowerShell, while similar, is also a completely different tool. If you understand the basic concepts of scripting, PowerShell is easy to pick up, but the syntax is different and can be a tripping point for more experienced script writers.
This blog series is meant as a guide for the person who is new to PowerShell but doesn’t know where to start. Consider this a cheat sheet to go from the basics to building more complex scripts. This will be an open-ended series – there’s no set end point. The order of information presented will follow the lessons I would use to teach a young systems administrator how to be more proficient with PowerShell. They are intended to help you learn but are not all-encompassing.
I will start with the basics – what is PowerShell? How do I access it, and how do I run basic CmdLets? In future posts I will start with a basic CmdLet, build it into a simple script, and then build that script into a more complex script with functions, logging, and error handling. This series is meant to be a practical, hands on exploration of PowerShell for IT Pros that need to quickly get up to speed. My hope is that you will take these lessons and build your knowledge from here.
The Basics
So, what is PowerShell?
Wikipedia defines PowerShell as, “… a task automation and configuration management framework from Microsoft, consisting of a command-line shell and associated scripting language.”
Cool. What does that mean?
PowerShell uses simple commands that use a verb-noun pairing to execute code. These are called CmdLets. The command shell looks very similar to a stand command prompt. You can run individual CmdLets or group them together into a script.
One of the unique features of PowerShell is the pipeline. You can run multiple CmdLets in a single string, passing the results from one CmdLet into the next using the pipeline character [|]. The pipeline is a powerful tool that allows you to run complex tasks quickly in a single line of code.
An administrator can be very effective with PowerShell using only basic CmdLets or scripts found online. Learning how to customize or write your own scripts will change the way you approach many complex tasks. As with any scripting language, you can automate many repetitive tasks that will free up your time to dive into more complex issues. Scripts can be as simple as a single CmdLet saved for later use, a string of CmdLets that run in sequential order, or contain functions that allow you to call sections of your script with different parameters.
Scripts can be developed into more advanced tools with a custom GUI or integrated directly into your PowerShell environment by building them into modules. A PowerShell module can be imported into an individual session or installed locally. Importing a PowerShell module lets you call functions like you would any other CmdLet.
That’s great – thanks for the lesson, but where do I begin?
I suppose the best place to begin is by opening PowerShell. There are two native options built into Windows for using PowerShell – the PowerShell console, and the PowerShell ISE (Integrated Script Editor). At first glance, the console looks like a basic command line. It works well for running individual CmdLets or calling pre-canned scripts.

I prefer to use the PowerShell ISE. It is a basic script editing utility that includes a console, a script editing pane, and a Command library. You can run single CmdLets by entering them in the console. You can open a script and edit it in the script pane. If you need to find a CmdLet you can search for Commands in the Command library. The ISE is a single tool that can be used for all of your PowerShell needs.

There are also third-party editors available for working with PowerShell. VS Code is a popular option used by many PowerShell enthusiasts, but for the sake of this series I will use the native tools available in the operating system. You can launch both environments by opening the Start menu and searching for PowerShell.
Running basic CMDLets
CmdLets are basic commands that are defined by a verb-noun pair. These are generally straightforward. Once you learn the basic syntax and common CmdLets many of these will become second nature. To run your first CmdLet open the PowerShell console and type Get-Host. In this case we want to get, or return, basic information about the PowerShell host, or console.
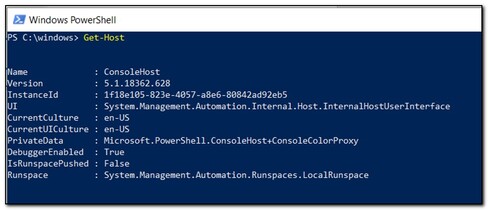
This seems like a very basic CmdLet. At first glance it may not seem to be the most helpful CmdLet, but over time you will find it is very useful. PowerShell is constantly being updated and new CmdLets are being added. If you attempt to run a CmdLet and it doesn’t work your PowerShell version may be out of date.
The “Host” is the instance of PowerShell you are running. Get-Host gets important information about your session. In the above example we use Get-Host to return a list of properties, in this case we can see that the host version is 5.1.18362.628. It is possible to return just the version. There are a lot of different ways to do that, but for this example we are going to use a pipeline [|] to pass the result of Get-Host into our next CMDLet, Select-Object.
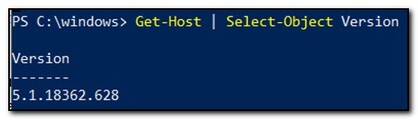
This keeps the entire CMDLet on one line. In this case we are using Select-Object to only select the Version property that was returned by Get-Host.
There are a lot of different ways to accomplish the same task in PowerShell. The pipeline keeps multiple commands on one line. PowerShell is an object-oriented scripting language. Get-Host returns the host information as an object. The pipeline passes the entire object into the Select-Object CmdLet, which processes the entire object and returns the Version object we requested. This line is clear, concise, and returns the exact value we need in one line. Alternately you could pass the result of Get-Host into a variable, and return the version property by using the following syntax:
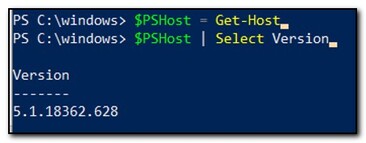
The results are the same, but this required two separate lines to accomplish the same task. If all you’re doing is trying to find the host version to for troubleshooting a specific issue the first option using the pipeline makes the most sense. There are other times, for example running a script with specific host requirements, where you may want to save the host as a variable first.
You may have also noticed that in this example I didn’t use Select-Object. Many PowerShell CmdLets have aliases, or shorthand ways of using the command. In this case “Select” is an alias of “Select-Object.” Many CmdLets have aliases, and you can even configure your own for commonly used commands.
One last thing
This wouldn’t be a proper basic tutorial if I skipped one final exercise. We commonly need to write output to the console. To do this, we use a CMDLet that will write output to the console. If you’ve been following along you may already know where this is going. Remember that CmdLets are named as verb-subject pairings. In this case we want to do something, “Write,” a value to the console, or in this case, the “host.” Our CmdLet for this is write-host.

So, that’s it, at least until next time.
This was, as promised, a very basic tutorial on PowerShell. It is an introduction to my series on PowerShell, which follows the method I use to teach new IT pros how to become more proficient at scripting. I want to develop IT Pros who are self-sufficient and believe the best way to do that is to provide the basic information they need to get started and practical lessons to help them continue to build their skills. These lessons will be cumulative – they will move quickly, and each one will build on the last one.
If you are looking for more in-depth resources, there are several excellent tools available. Here are several this I recommend:
Books
Learn Windows PowerShell in a Month of Lunches by Don Jones and Jeffery Hicks
PowerShell for Sysadmins by Adam Bertram
Video Series
Microsoft PowerShell for beginners – Shane Young

